A few tricks to better understand and use the S/(S+V) formula in ComPressure.
The S/(S+V) Formula Deciphered
When unlocking the 11th help promptly, you get told that for a setup like this, if we call S the openness of the valve connected to the inlet, and V the openness of the valve connected to the air, the output pressure is:
(S ÷ (S+V)) 100 PSI
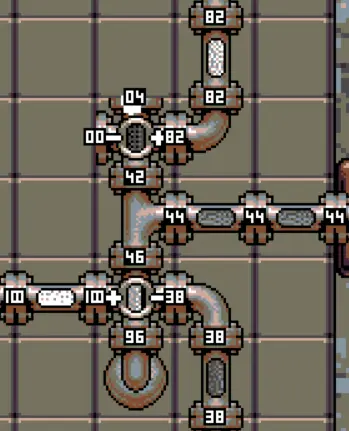
As many of you have experienced, this is not exact. Just on the picture, you can calculate : V = 82 and S = 100 – 38 = 62. Applying the formula, we find S/(S+V) ≈ 43,1%, and yet the output is 44 PSI.
For lighter notations, we will, in all the following, write X = output ÷ (100PSI) and also introduce the value α = 533,333… = 1600÷3 (it is a secret tool that will help us later).
The exact formula is, and I ask you to trust me on this,
X = S × (V + α) ÷ (2×SV + α(S+V) )
With the values on the picture, it gives X ≈ 43,9 which gets displayed as a 44 PSI.
One other thing you should remark is that it not a terribly bad approximation. Actually, X and S/(S+V) are rather close :
X - S/(S+V) = [S×V×(V-S)] ÷ [(2×S×V + α×(S+V)) × (S+V)]
But one should note that the difference only vanishes in three cases : if S = 0 (in which case X = 0%), V = 0 (X = 100%) and X = V (X = 50%). In other words, the only three values that we can produce exactly are 0 PSI, 50 PSI and 100 PSI.
In the following section, we will discuss where this formula came from, and how to slightly improve its precision.
The Generalized Formula
If you have a pair of blocks arranged like this, it is actually possible to find the value at the equilibrium of the middle point. For this, I like to proceed to an electrical analogy.
Each pipe can be viewed as electrical resistance, with a resistance of 2δ:1δ to go from an extremity to the middle point, and 1δ to go from the middle point to another extremity. An inlet also has the same resistance: it is quite literally a pipe at the end of which lies a perfect source of 100PSI. And the air as well as a resistance of 2δ, for the sake of symmetry.
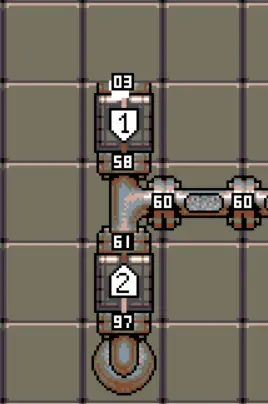
So for any pipe, the flow of steam going through the extremity of a pipe is proportional to the difference of pressure between its middle value (the average of its pressures at extremities) and said extremity, with a factor of δ.
The value of δ actually does not matter at all here; it just is the ratio, but for those who want to know, it is actually equivalent to a duration: δ is 1/10000 of the “Tick” value from the clock level.
Now if we call R1 the resistance of block 1 and R2 the resistance of block 2, then the value in the middle is
X = (R1+3δ) ÷ (R1+R2+6δ)
There is an extra 3δ on each side because 2δ is brought by the air/inlet, and there is 1δ on each side of the pipe at the junction.
Note that if the 2 blocks are identical (for instance, by not being there), we find X=50% and that’s probably how you solved the “50” level.
But now, one element is missing: what is the resistance of a valve? Through many serious experiments (such as: asking the developer of the game), I have found that the resistance of a non-closed valve is 1600×δ÷openness = 3δ×α÷openness. (The resistance of a closed valve is meaningless since there is no stream flowing through, and thus we don’t have to worry about what happens when a division by 0 occurs). One observation that I would like to make, is that S/(S+V) is what you get if you just ignore the +3δ
Now, plugging in a valve of openness V and a valve of openness S as block 1 and block 2, we get:
X = (3δ×α÷V + 3δ) ÷ (3δ×α÷V + 3δ×α÷S + 6δ)
You can check for yourself that it becomes the formula I gave in the previous section. But one observation that one could make, is that S/(S+V) is what you obtain by ignoring the +3δ and +6δ.
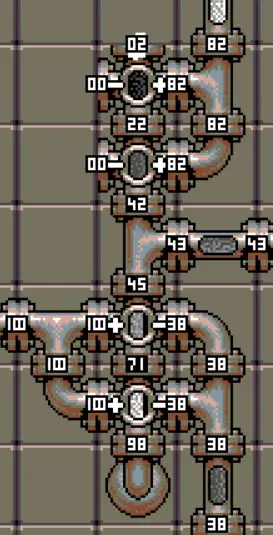
One way of fighting this error term is by making the resistance of the relevant parts relatively bigger. Here, by doubling down the valves, the +3δ gets relatively twice as small.
In terms of output, we fare better than during the previous section: we are just below 43,5; which is better than the 43,9 we had previously, but still not exactly the 43,1 we would want.
One could go a step further and make the same setup with triple valves. It gets a bit closer but I would not recommend it, because each additional layer of valves makes the throughput worse.
In the next section, we will discuss how to break free from this inherently inexact ratio. But it requires elaborate techniques, and for some levels, such as level 20, those are not applicable and you will have to use the S/(S+V) formula, or its cousin that we discussed here.
Beyond the Formula
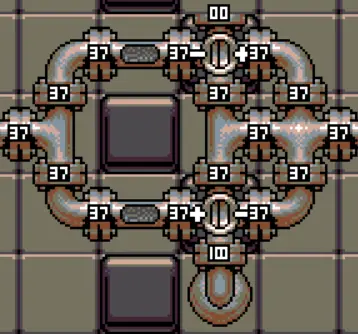
What happens to an S/(S+V) setup when both valves are closed? The pressure stops evolving, stays at its current value until at least one of the valves becomes open again.
Previously we have seen that there will always become errors while we’re in the scope of the formula. So our only way to exactness is to step out of the formula altogether.
One the picture, you can see a simple model of “exact buffer”: this buffer always evolves towards the exact same value as its input, because when it reaches it, both valves become closed and there is no evolution anymore. Its main downside is that it is really slow to reach very high and very low pressures, and ends up with a worse score than the basic inaccurate buffer. Still, it is in my humble opinion a better design to use as a subcomponent.
This technique is primordial, and gets expanded upon, starting from the levels “Decrypt” and “Sensor”: almost any comparator, when comparing two exactly equal values, will have both their valves closed. Which means that their current values will be preserved even if it is not 0 or 100.
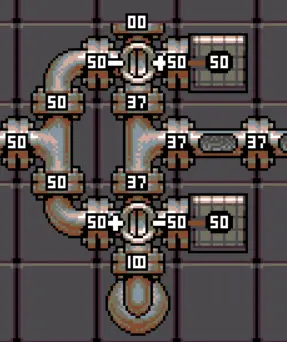
Now, an Amp50 will “close” this way if the value it gets as input is exactly 50. And, luckily, the conclusion of the first section was the only three values that we can produce exactly are 0 PSI, 50 PSI, and 100 PSI.
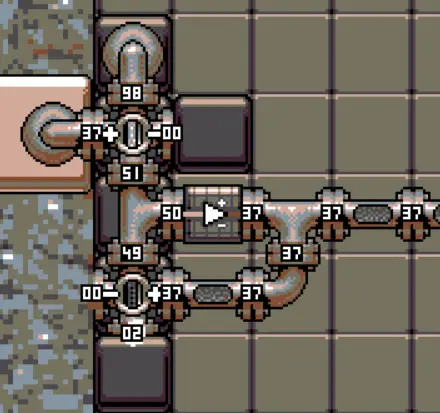
The sensor gives us a way to exactly replicate a pressure and more generally the openness of a given valve. It is an extremely useful technique that comes up in a lot of levels, such as Adder or Subtractor. And who knows, maybe you could even use it to get a better score in the “buffer” level?
That's everything we are sharing today for this ComPressure guide. This guide was originally created and written by Akiel. In case we fail to update this guide, you can find the latest update by following this link.
